0196-4ACh4. Efficacité d’un échangeur contre-courant huile/eau

Un ensemble moteur (voir figure ci-dessous) est refroidi, en régime permanent, par la circulation forcée d’un fluide caloporteur (huile moteur), à un débit de 1200 L/h. Ce fluide est refroidi par un échangeur externe fonctionnant à contre-courant. Il parcourt le tube intérieur d’un échangeur coaxial, à contre-courant avec de l’eau de refroidissement, circulant en double enveloppe, à un débit de 1600 L/h. Le fluide caloporteur entre dans l’échangeur à la température de 140°C, et doit être refroidi à la température de 80°C. L’eau de refroidissement est disponible à la température de 10°C.

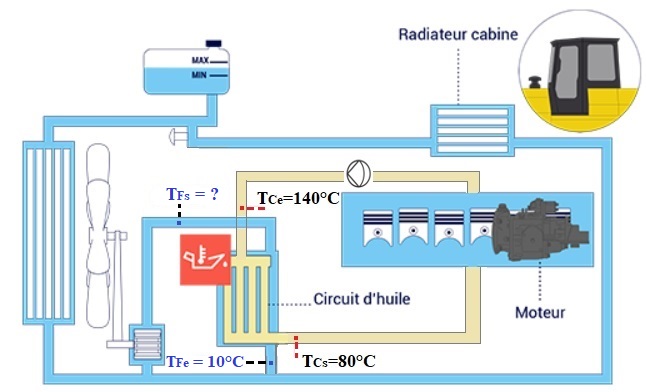
Le tube intérieur de l’échangeur a un diamètre intérieur D_int = 12 mm, et une épaisseur e = 1 mm. Il est en acier inox, de conductivité thermique λ_inox = 10 W/m°C.  La double enveloppe a un diamètre intérieur qui permet d’imposer une conductance de transfert h_ext sur le tube intérieur de 5000 W/m²°C (paroi extérieure du tube intérieur/ eau). L’ensemble est supposé parfaitement isolé extérieurement.

1°) On prendra, pour le fluide caloporteur, à sa température moyenne, une masse volumique moyenne de 840 kg/m³, une chaleur spécifique moyenne de C_P = 2200 J/kg°C, une viscosité dynamique µ = 1,68.10^-3 kg.m^-1.s^-1, et une conductivité thermique λ = 0,14 W/m°C.

• Déterminer le nombre de Prandtl P_r, du fluide caloporteur.

2°) Calculer le nombre de Reynolds R_e, de l’écoulement du fluide caloporteur.

3°) En déduire la conductance de transfert h_int (caloporteur/paroi intérieure du tube intérieur).

4°) En déduire la conductance globale de transfert U_ext, de l’échangeur, rapportée au diamètre extérieur du tube intérieur.

5°) Calculer la puissance thermique P_th de l’échangeur.

6°) Déterminer la longueur L(m) de l’échangeur.

7°) Calculer la perte de charge ∆P_f (bars) du fluide caloporteur, entre l’entrée et la sortie de l’échangeur. En déduire la puissance mécanique minimum P_m d’une pompe, placée en amont de l’échangeur, destinée à imposer le débit du fluide caloporteur, en régime permanent.

On pourra utiliser la corrélation de Blasius (ou toute autre corrélation), en conduite lisse et en régime turbulent.

• Déduire le rapport : eff = P_th / P_m. Conclure

8°) Déterminer alors l’efficacité de l’échangeur par un modèle plus approprié

On donne, pour l’eau : chaleur spécifique : 4,18 kJ/kg°C, masse volumique : 1000 kg/m³.