0230-3ACh1. Quelques aspects thermiques de la Lune*

La Lune est le satellite naturel de la Terre. On s’intéresse ici à quelques aspects thermiques de la Lune, en particulier de la surface lunaire. On fait hypothèse que la Lune, la Terre et le Soleil sont assimilés à des sphères en équilibre radiatif. Et on considère que ces objets échangent de l’énergie avec l’extérieur uniquement par rayonnement thermique.

Le problème posé ici se décompose en deux parties indépendantes et les données relatives à ce problème sont fournies ci-dessous.

Le Soleil sera assimilé à un corps noir et la Lune, considérée comme un corps opaque dont le rayonnement émis est assimilé à celui d’un corps noir. L’albédo moyen de la Lune, A_L, est égal à 0,073, ce qui signifie que 92,7% du flux solaire est absorbé par le sol. On suppose l’albédo uniforme sur toute la surface éclairée.

La Terre est modélisée comme un corps opaque dont le rayonnement émis est celui d’un corps noir. L’atmosphère est modélisée par une couche d’épaisseur e << R_T, avec R_T le rayon de la Terre. Le rayonnement émis par l’atmosphère est assimilé à celui d’un corps noir à la température T_atm supposée uniforme. On notera A_T l’albédo du système {Terre + atmosphère}. On notera D_ST la distance Soleil-Terre, et D_SL la distance Soleil-Lune.

Partie I : Rayonnement et température lunaire

1°) Exprimer le flux émis ϕ_S par le Soleil en fonction notamment du rayon solaire R_S et de la température solaire T_S.

2°) Établir l’expression de la température de surface de la Lune, notée T_L, Soleil et supposée uniforme, en ne tenant compte que du rayonnement solaire. Montrer qu’elle se met sous la forme :

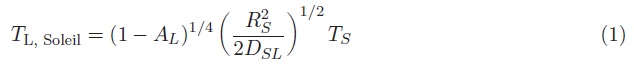
L’hypothèse d’une température uniforme pour la Lune n’est pas conforme à la réalité car la surface lunaire présente de gros écarts de température. Dans la zone de températures les plus élevées, il est possible de montrer (non demandé ici) que la température maximale T_L,max à la surface de la Lune est donnée par :

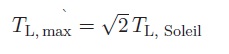
3°) Représenter sur un schéma la position, par rapport au Soleil, de la zone de températures les plus élevées. Calculer T_L,max et commenter sachant que la valeur expérimentale est de l’ordre de 120°C.

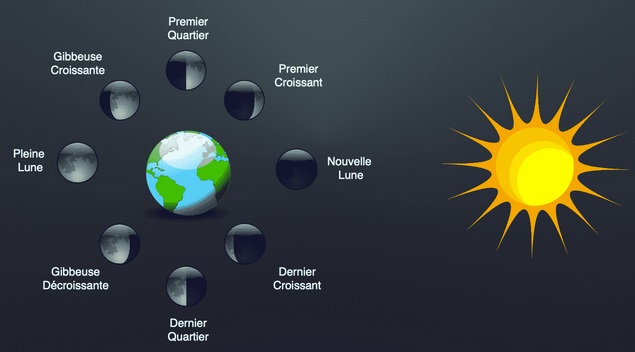
Lorsque l’axe Soleil-Terre est perpendiculaire à l’axe Lune-Terre (Lune positionnée au Premier-Quartier ou au Dernier-Quartier, voir figure ci-dessus), on cherche à déterminer la température superficielle de la Lune en un point M éclairé uniquement par la Terre (voir figure ci-dessous). Ce point reçoit le rayonnement de deux corps de nature différente qui émettent comme des corps noirs : celui du Soleil, réfléchi par le système {Terre + atmosphère} et celui émis par l’atmosphère terrestre.

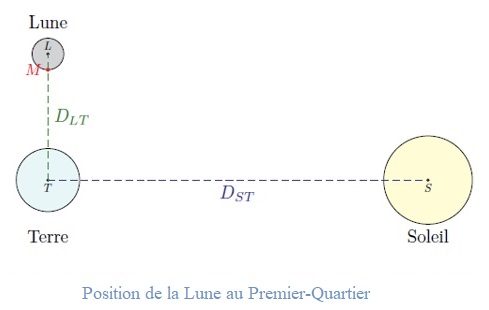
4°) Exprimer la densité de flux de chacun de ces rayonnements. On notera φ_{S, ref ,T} la densité de flux solaire réfléchi par la Terre qui arrive sur la Lune et φ_{atm ,T} celle provenant l’atmosphère terrestre.

5°) Exprimer, puis calculer, la température à la surface de la Lune uniquement éclairée par la Terre, notée T_L,_Terre.

6°) Un instrument situé à la surface de la Lune détecte le rayonnement incident dans les domaines du visible et de l’infrarouge. Indiquer, en micromètres, le domaine de longueurs d’onde caractéristique de chacun de ces rayonnements.

7°) À quel domaine de longueurs d’onde appartient le rayonnement thermique émis par la Lune ? Quelle est l’origine du rayonnement visible provenant de la Lune ?

La Lune contient des roches radioactives, essentiellement ²³⁸U et ⁴⁰K qui, en se désintégrant, fournissent une certaine quantité de chaleur. Ainsi, pour ce phénomène, la puissance volumique moyenne libérée par les roches lunaires, P_L, a été évaluée à 10^-8 W·m^-3.

8°) Exprimer la température superficielle de la Lune, T_{L, roches}, pour les zones à l’ombre du Soleil et de la Terre et en ne tenant compte que de l’apport énergétique radioactif.

9°) La radioactivité modifie-t-elle de façon significative la température dans les zones très éclairées ?

Partie II : Stabilité du sol lunaire

La composition du sol lunaire est proche de celle des silicates. On fait ici l’hypothèse d’une Lune homogène et de caractéristiques physiques identiques à celles des silicates. La température de tout point de la Lune est indépendante du temps. La température de surface est T_s,L = 290 K. La puissance volumique moyenne libérée par les roches lunaires est évaluée à P_L = 10^-8 W·m^-3. On note K_Sil la conductivité thermique des silicates.

Formulaire : Opérateur LAPLACIEN scalaire en coordonnées sphériques

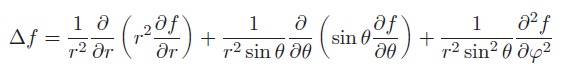
10°) Établir l’expression de la température donnée par :

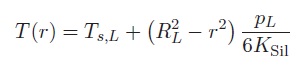
11°) Calculer la température au centre de la Lune. Que peut-on prévoir pour l’état de la roche dans cette région ?

12°) À la pression atmosphérique terrestre, la température de fusion des silicates est proche de 1500K. Compte tenu de cette donnée, évaluer l’épaisseur du manteau solide de la Lune. Cette épaisseur, ainsi calculée, est inférieure à l’épaisseur véritable. Quelle est la principale faiblesse de ce modèle rudimentaire ?

13°) La radioactivité de la Lune est essentiellement liée au potassium 40 de période radioactive proche de 1,5 milliards d’années. La période radioactive est le temps au bout duquel la puissance radioactive a diminué de moitié. Donner un ordre de grandeur de l’épaisseur du manteau solide lors de la formation de la Lune, il y a 4,5 milliards d’années.