Un système d’ailettes de section carrée (voir figure ci-dessous), de côté c = 0,2mm, de longueur L = 5mm et séparées de d = 0,15mm est attaché à un circuit imprimé de forme carrée (de côté Z = 10,35mm) pour augmenter la puissance maximale du circuit sans dépasser une température maximale TM = 80°C. Les ailettes sont solidaires d’un support d’épaisseur e = 3mm, lui-même fixé sur une face du circuit imprimé. On suppose que le circuit imprimé est isolé sur les autres faces.
Le refroidissement est assuré par la circulation d’un liquide à la température T1 = 20°C avec un coefficient d’échange convectif h = 1200W·m−2·K−1. La conductivité thermique du support et des ailettes est λ = 450W·m−1·K−1. On suppose que la température du support est uniforme sur toute tranche perpendiculaire à son épaisseur. On notera T0 la température de la surface du support en contact avec les ailettes, et on suppose que le contact est parfait. On néglige les échanges convectifs en bout d’ailette.
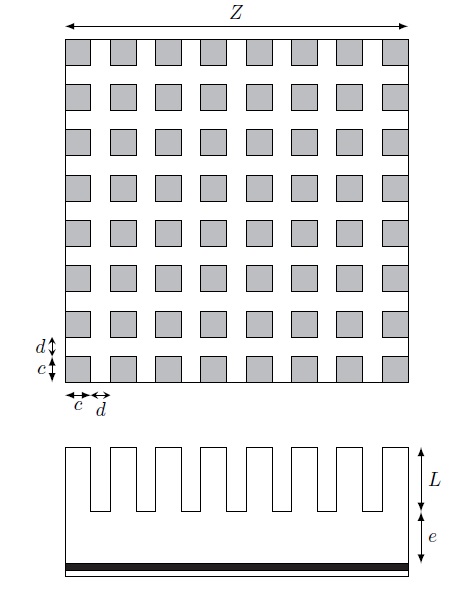
ATTENTION : l’échelle et le nombre d’ailettes ne sont pas respectés sur cette figure
On donne respectivement les expressions de l’efficacité et du module d’une ailette (où p est le périmètre mouillé de l’ailette et A l’aire de sa section droite) :
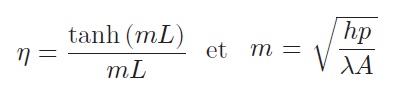
1-) Calculer m et ƞ
2-) Exprimer la puissance dissipée par une seule ailette en fonction de T0 et des données du problème
3-) Exprimer, puis calculer, la résistance thermique Ra d’une ailette seule
4-) Exprimer, puis calculer, la résistance thermique RS du support seul
5-) Donner l’expression de la résistance thermique Req du système d’ailettes avec son support
6-) Déterminer N, le nombre d’ailettes du système puis, calculer Req
7-) Calculer alors la puissance maximale dissipée entre le support et le circuit
8.-) En déduire T0
9-) Que devient l’expression de la résistance globale dans le cas où l’on tient compte d’une résistance de contact non nulle entre le support et le circuit. On ne demande pas d’application numérique
