0197-4ACh3. Efficacité du Circuit secondaire d’une centrale nucléaire – cycle de Rankine*

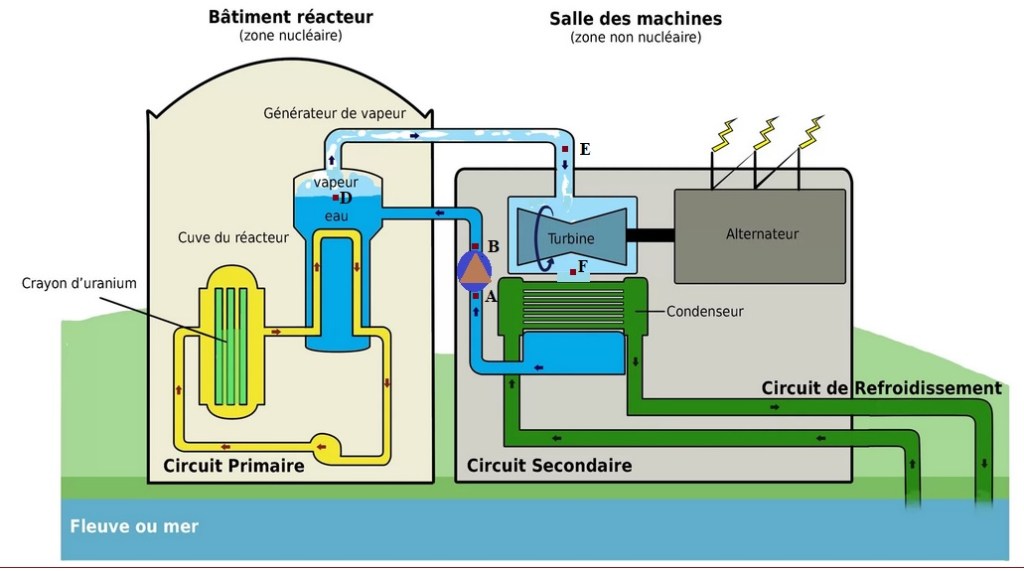
L’objectif de ce problème est de caractériser la performance du circuit secondaire d’une centrale nucléaire (voir figure ci-dessous).

On désigne par p la pression du système liquide-vapeur et par v son volume massique. L’équilibre entre l’eau liquide et sa vapeur est caractérisé, à différentes températures, par les données suivantes dont les valeurs numériques sont données dans le Tableau 1 :

On définit par

• θ  : température en °C ;
• p  : pression de vapeur saturante ;
• v_L : volume massique du liquide saturant ;
• v_G : volume massique de la vapeur saturante ;
• h_L : enthalpie massique du liquide saturant ;
• h_G : enthalpie massique de la vapeur saturante ;
• s_L :  entropie massique du liquide saturant ;
• s_G : entropie massique de la vapeur saturante.

NB : Dans tout cet énoncé, on se placera en régime permanent conservatif. De plus, les variations d’énergie cinétique et potentielle seront considérées négligeables. Tous les calculs se rapporteront à une masse m = 1 kg de fluide. La capacité thermique massique c_L du liquide est constante et vaut 4,18 kJ·kg⁻¹·K⁻¹. Le coefficient de dilatation isobare α de l’eau liquide, supposé constant, vaut 1,5 × 10⁻⁴ K⁻¹.

Le circuit secondaire de cette centrale nucléaire (voir figure ci-dessus) comporte les éléments suivants :

• Un générateur de vapeur,
• Une turbine,
• Un condenseur,
• Une pompe d’alimentation.

Les transformations subies par l’eau dans ce circuit sont modélisées par le cycle de Rankine décrit ci-dessous

• A→ B : compression adiabatique réversible, dans la pompe d’alimentation, du liquide saturant sortant du condenseur de la pression p₁ = 0,0562 bar, à la pression p₂ = 69,2 bar. Cette compression entraîne une élévation ΔT de la température du liquide.

• B→ D : échauffement isobare du liquide dans le générateur de vapeur qui amène le liquide de l’état B à l’état de liquide saturant sous la pression p₂ (état D).

• D → E : vaporisation totale (vapeur saturante sèche), dans le générateur de vapeur, sous la pression p₂.

• E →F : détente adiabatique réversible, dans la turbine, de p₂ à p₁.

• F → A : liquéfaction totale, dans le condenseur, sous la pression p₁, de la vapeur présente dans l’état F

1-) Représenter le cycle décrit par l’eau dans le diagramme de Clapeyron (p, v). Est-il moteur ou récepteur (justifier votre réponse) ?

2-) Transposer le cycle précédent dans un diagramme entropique (T,s).

La différentielle de l’entropie massique du liquide s’écrit, en fonction des variables T et p par :

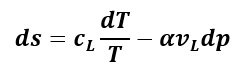
On note : ΔT = T−T₁, l’élévation de la température du liquide dans la pompe d’alimentation, sachant que ΔT << T₁.

3-) Exprimer de 2 façons différentes la différence de température ΔT, puis la calculer , conclure. On supposera pour ce calcul, que le liquide est incompressible et que son volume massique v_L = 10⁻³ m³·kg⁻¹.

Dans la suite du problème on négligera ΔT devant T₁.

4-) Il est rappelé que le titre massique en vapeur x d’un système liquide-vapeur est égal au rapport entre la masse m_G d’eau à l’état de vapeur saturante et la masse totale m du système. On désigne, respectivement par : v_m et h_m, le volume massique et l’enthalpie massique du système liquide-vapeur correspondant à un point M du palier de saturation.

• Retrouver l’expression du titre massique en vapeur x, en fonction de : h_m, h_L et h_G.

• En déduire (expression littérale et application numérique), l’enthalpie massique h_F du système liquide-vapeur sortant de la turbine (état F)

5-) En raisonnant à partir du bilan d’énergie entrée/sortie de la pompe (Premier Principe de la Thermodynamique en circuit ouvert) ou d’une toute autre méthode (Relation de Gibbs par exemple),

• Exprimer le travail massique w_p fourni par la pompe au fluide en fonction de v_L, p_A et p_B. Avec v_L le volume massique du liquide supposé incompressible
• Calculer la valeur numérique de w_p et comparer ce travail au travail spécifique de la turbine

6-) Exprimer et calculer les transferts thermiques q₁ et q₂ reçus par 1 kg d’eau respectivement, dans le condenseur et dans le générateur de vapeur.

7-) Exprimer et calculer le travail w_u reçu, par 1 kg de fluide et en déduire le rendement thermodynamique du cycle.

8.-) Comparer ce rendement à celui d’un cycle de Carnot décrit entre les mêmes températures extrêmes T₁ et T₂. Conclure