0199-3ACh2. Conduite cylindrique de transport de bitume*

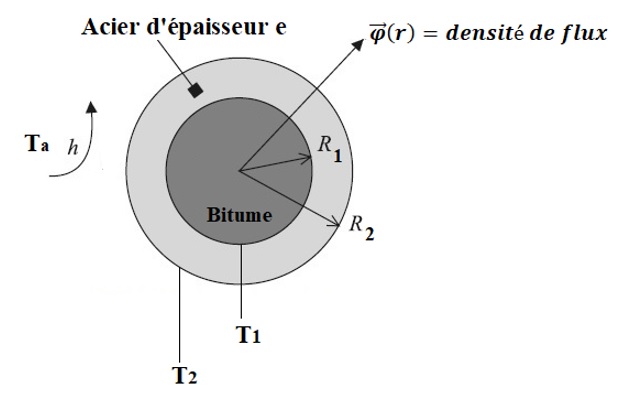
On utilise pour alimentation en bitume du malaxeur d’une centrale d’enrobage, une conduite cylindrique en acier (voir figure ci-dessous). Le diamètre intérieur de la conduite est de D₁ = 100 mm et son épaisseur est de e = 10 mm. La température T₁ de la surface intérieure du tuyau est de 120°C. La température de la surface extérieure est notée T₂ (inconnue). On supposera que la couche en acier est homogène, la longueur L = 1 m est grande par rapport aux rayons R₁et R₂ (R₂ = R₁ + e) et la conductivité thermique de l’acier λ_a, est indépendante de la température en régime établi. La température ambiante est de T_a = 16°C. Le coefficient de convection sur la face extérieure en contact avec l’air ambiant est de h = 15 W/m².K.

1-) A partir de l’équation de la chaleur en régime permanent sans terme source (pas de production de chaleur), déterminer l’expression analytique du profil de température T(r), pour r variant de R₁ à R₂.

2-) Quel est l’expression du flux de chaleur perdu, pour r variant de R₁ à R₂ ? que peut-on en conclure ?

3-) Déterminer alors une expression du flux perdu en fonction de : T₁, T_a, R₂, R₁, L, λ_a et h uniquement. Calculer sa valeur.

Afin de limiter la consommation d’énergie, on décide d’isoler la conduite à l’aide d’une gaine isolante d’épaisseur e_is = 5 cm. La valeur de la conductivité thermique de l’isolant est :

λ_is = 0,91 W.m^-1.K^-1

4-) Déterminer une expression de la résistance thermique totale R_tot, du complexe : acier-isolant-air. En déduire une expression du flux thermique perdu en fonction de R_tot et calculer sa valeur.

5-) Calculer alors le gain en (%), réalisé après la pose de l’isolant.

6-) Montrer qu’à paramètre constant, à l’exception de l’épaisseur de l’isolant e_is, la fonction R_tot(e_is) passe par un minimum local. En déduire la valeur numérique de l’épaisseur de l’isolant associée à ce minimum.