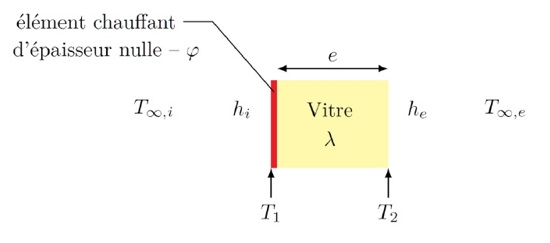
Pour dégivrer la vitre arrière d’une voiture, une couche très fine (épaisseur négligeable) transparente d’un élément chauffant est placée sur la surface intérieure de la vitre. Cet élément chauffant produit une densité de flux 𝜑 = 1300 𝑊⋅𝑚−2 permettant de dégivrer la vitre d’épaisseur 𝑒 = 5 𝑚𝑚 et de conductivité thermique 𝜆 = 1,2 𝑊⋅𝑚−1⋅𝐾−1. On notera 𝑆 la surface de la vitre.
La température à l’intérieur de l’habitacle de la voiture est 𝑇∞,𝑖 = 22°𝐶 et le coefficient de transfert convectif est ℎ𝑖 =15 𝑊⋅𝑚−2⋅𝐾−1. La température à l’extérieur est 𝑇∞,𝑒 = − 5°𝐶 et le coefficient de transfert convectif est ℎ𝑒 = 100 𝑊⋅𝑚−2⋅𝐾−1.
On note 𝑇1 la température de la surface interne de la vitre, et 𝑇2 la température de la surface externe de la vitre. L’étude se place sous l’hypothèse de régime permanent.
1-) Rappeler les conditions pour pouvoir utiliser la notion de résistance thermique
2-) Réaliser le schéma électrique équivalent de la situation étudiée. Faire apparaître les températures (notations) et préciser les expressions des résistances thermiques introduites
3-) Exprimer le flux thermique perdu à l’intérieur de la voiture
4-) Exprimer le flux thermique transféré vers l’extérieur de la voiture en fonction de 𝜆, ℎ𝑒 et des autres paramètres de l’énoncé que vous jugerez utiles
5-) Écrire une relation entre la densité de flux 𝜑, le flux thermique perdu à l’intérieur et le flux thermique transféré vers l’extérieur de la voiture
6-) Déterminer une expression de la température 𝑇1 de la surface interne de la vitre. Montrer qu’elle peut se mettre sous la forme :
𝑇1 = 𝛼[𝜑 + 𝛽𝑇∞,𝑒 + 𝛾 𝑇∞,𝑖]
- Préciser les expressions de 𝛼, 𝛽 et 𝛾
7-) Calculer 𝛼 et 𝛽 (attention aux unités !). Calculer 𝑇1
8.-) Quelle serait la valeur de 𝑇1 en l’absence de l’élément chauffant ?

Bonjour ou pourrais – je trouver les corrigés ?
J’aimeJ’aime