Le problème traite de la mesure de la température d’un corps. Plus précisément, ce problème va permettre d’étudier la méthode Photothermique. Cette dernière présente un intérêt dans certaines applications où la mesure d’une température à l’aide d’un thermomètre de contact est impossible (températures élevées, objets éloignés,…).
La méthode Photothermique de mesure de la température T0 d’un corps solide opaque consiste à perturber localement le champ de température T(r,t) de ce corps par un apport d’énergie lumineuse variable notée Jλo(t). Cette énergie lumineuse est fournie par un faisceau laser cylindrique monochromatique de longueur d’onde λ0 dans le vide et de section transversale ∆S.
En présence du faisceau laser, le corps émet localement un rayonnement thermique de température T(r,t) qui est analysé par un détecteur photométrique. On considère le dispositif expérimental représenté dans la figure ci-dessous. L’échantillon Σ dont on souhaite mesurer la température T0 est un solide opaque, cylindrique de section circulaire ∆S et d’épaisseur e = 1 cm. La paroi latérale de l’échantillon est supposée parfaitement calorifugée par un corps athermane. La face supérieure (FS) de l’échantillon est à l’air libre de température Ta.
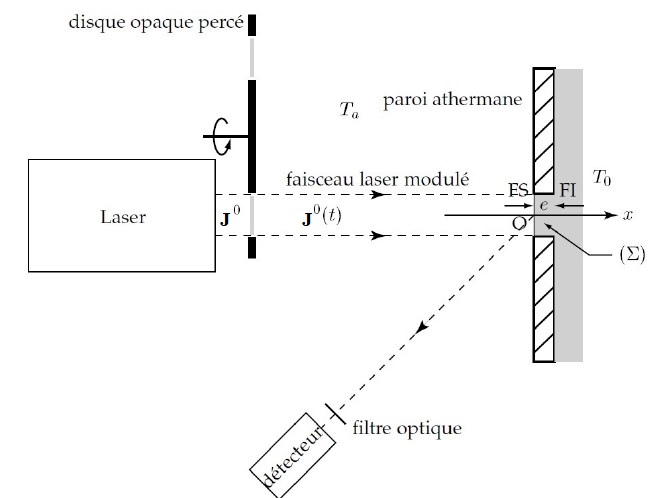
L’air ainsi que tous les milieux traversés par les divers flux lumineux sont supposés parfaitement transparents. Tous les instruments de mesure supposés à la température constante Ta. On appelle h, supposé constant, le coefficient de transfert convectif entre (FS) et l’air. La face inférieure (FI) de l’échantillon est en contact thermique parfait avec un thermostat de température constante T0.
Du fait de l’éclairage ambiant, le solide est soumis en permanence à un flux lumineux parasite Jpa qui apporte au corps une très faible énergie thermique. Les propriétés radiatives de Σ sont modélisées par celles du corps noir. On note c la capacité thermique du solide, λ sa conductivité thermique et ρ sa masse volumique. Toutes ces grandeurs seront supposées constantes. On note σ la constante de Stefan-Boltzmann.
Partie I : Étude de l’équilibre thermique initial
On considère tout d’abord la situation initiale où le solide n’est pas éclairé par le faisceau laser. Dans ces conditions, le corps est en équilibre thermique à la température T0 constante.
1-) En précisant la loi utilisée, exprimer la densité de flux Je-CN émise par le corps noir à la température T0.
2-) Après avoir déterminé les différents flux mis en jeu dans l’étude, montrer à l’aide d’un bilan d’énergie, que la température initiale T0 du solide, supposée uniforme vérifie l’équation suivante :
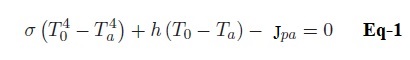
3-) La faible valeur de Jpa implique que la température T0 du corps est très légèrement supérieure à la température ambiante Ta. Montrer alors que l’on peut linéariser l’Eq-1, sous la forme :
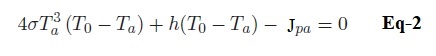
Partie II : Bilan d’énergie en régime variable
On considère le solide Σ. On suppose que sa température est variable et peut s’écrire sous la forme T = T(x,t), du fait d’un apport d’énergie thermique surfacique variable, à l’interface entre (FS) et l’air libre en x = 0.
4-) Établir que l’équation vérifiée par la température T au sein de l’échantillon est donnée par :
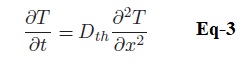
- Donner l’expression analytique et l’unité, de la diffusivité thermique Dth.
5-) On donne δt la durée de l’expérience pendant laquelle on impose un apport d’énergie thermique à l’interface entre (FS) et l’air libre. On donne par ailleurs : Dth = 10-6 SI et δt = 0,1 s. En partant d’une analyse aux dimensions de l’Eq-3, donner une expression de la longueur Lq de pénétration de l’énergie thermique par diffusion dans le solide, en fonction de Dth et δt. Calculer Lq.
6-) En comparant la valeur de Lq à l’épaisseur e = 1 cm de l’échantillon, montrer que l’on a T(x,t) = T0, à chaque instant t de l’expérience, avec ici x >>> Lq.
Partie III : Résolution et conditions aux limites
On cherche à résoudre l’Eq-3 qui donne le champ des températures T(x,t) au sein Σ lorsque le solide est éclairé par le faisceau laser modulé, dont la densité de flux est J0(t). Le faible flux parasite Jpa, la température ambiante Ta et la température T0 du thermostat, sont supposés avoir les mêmes valeurs que dans la situation statique étudiée Partie I.
On pose la température absolue complexe sous la forme :
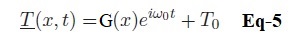
Avec G(x) une fonction complexe de la position x uniquement. On désigne par i, le nombre complexe que i2 = -1.
Par ailleurs, on a :
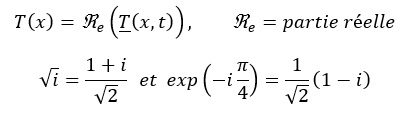
7-) Déduire des Eqs 3 et 5, l’équation différentielle vérifiée par G(x).
La solution de l’équation différentielle établie à la question précédente peut se mettre sous la forme :
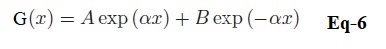
8.-) Donner une expression de la constante complexe a en fonction de w0 et Dth.
9-) Que peut-on dire de la température T(x >> Lq,t) de l’échantillon ? Justifier le fait que A est nécessairement nul.
Afin de déterminer la constante B, on admettra qu’à l’interface x = 0, il est possible d’écrire l’équation de continuité suivante :
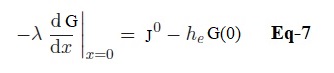
Avec, he = h + 4σTa3
On donne :
Dth = 10-6 m2.s-1 ; h = 20 W.K-1.m-2 ; σ = 5,67×10-8W.K-4.m-2 ; λ = 10 W.m-1.K-1 ; Ta = 300 K et f = w0/2π = 500 Hz.
10-) Montrer par un calcul d’ordre de grandeur que :
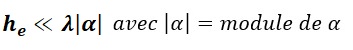
- Montrer alors que B peut s’écrire sous la forme :

11-) En déduire que :
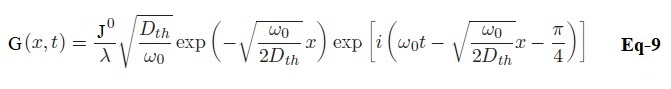
12-) Donner finalement l’expression du champ des températures T(x,t) dans le solide Σ. Discuter du sens physique de chacun des termes qui apparaissent dans T(x,t). Vérifier qu’en absence de faisceau laser, on retrouve la situation statique.
