0208-4ACh4. Encombrement d’un Échangeur Sodium – Eau*

On considère un échangeur à contre-courant de longueur L = 3 m fonctionnant en régime permanent (voir figure ci-dessous).

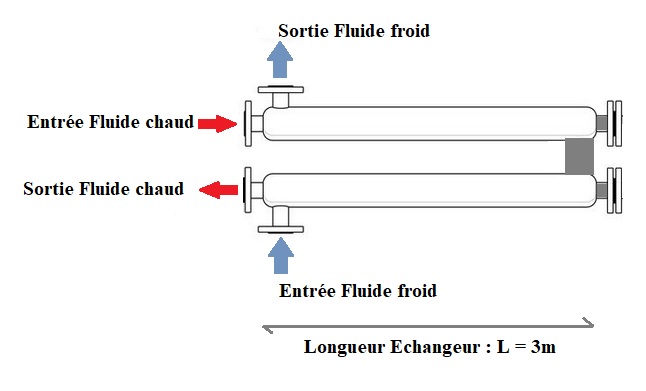
On suppose que le diamètre du tube intérieur est, D_int = 2 cm. Dans ce tube intérieur circule un fluide caloporteur (Sodium-liquide) dont les températures en entrée et en sortie sont respectivement T_calo,e = 200°𝐶 et T_calo,s = 110°C. Ce fluide avance à la vitesse V_calo = 0,67 m.s^-1. A l’extérieur de ce tube, circule de l’eau (Fluide-froid) dans un tube circulaire dont on cherche à exprimer le diamètre hydraulique (D_h) afin d’en déduire l’encombrement du système complet au travers de son diamètre (D_systeme = diamètre intérieur du cylindre extérieur). La température de l’eau à son entrée est T_eau,e = 30°𝐶 et sa température à la sortie est T_eau,s = 90°𝐶. On considère l’épaisseur e de la paroi séparatrice Eau – Fluide Caloporteur comme négligeable.
Données numériques pour le fluide caloporteur : ρ_calo = 910 kg.m^-1, capacité thermique massique c_p,calo = 1340 J.kg^-1.K^-1, viscosité dynamique μ_calo = 0,00052 kg.m^-1.s^-1 et conductivité thermique λ_calo = 84 W.m^-1.K^-1.
Données numériques pour l’eau : masse volumique ρ_eau = 980 kg.m^-3, capacité thermique massique c_p,eau = 4180 J.kg^-1.K^-1, viscosité dynamique μ_eau = 0,00043 kg.m^-1.s^-1 et conductivité
Thermique λ_eau = 0,65 W.m^-1.K^-1.

• On rappelle la Corrélation de Colburn : Nu = 0,023xRe^0,8xPr^1/3. Ses conditions d’application sont celles données dans le cours : 0,5 < Pr < 120 et 2300 < Re < 12.10⁴.
• On donne la Corrélation de Skupinski : Nu = 4,82 + 0,0185 x (Re x Pr)^0,827 et ses conditions d’application : 3.10^-3 ≤ Pr ≤ 5.10^-2, 3,6.10³ ≤ Re ≤ 9.10⁵ , 100 ≤ Re x Pr ≤ 10⁴ et L/D_int ≥ 30.

1) Déterminer le débit massique du fluide chaud dans la canalisation intérieure.
2) A partir du calcul du nombre de Reynolds (Re_calo), déterminer le régime de l’écoulement. Justifier votre réponse.
3) Déterminer la puissance calorifique cédée par ce fluide pour se refroidir et ainsi réchauffer l’eau.
4) Déterminer le nombre de Prandtl (Pr_calo) du fluide caloporteur.
5) En justifiant votre raisonnement, déterminer le nombre de Nusselt (Nu_calo) du fluide caloporteur
6) En déduire la conductance de transfert (h_calo) associée au fluide chaud.
7) Quel doit être le débit massique de l’eau pour assurer le refroidissement dans les conditions de fonctionnement ?
8) Compte tenu des données du problème, déterminer la différence logarithmique de température (DTLM).
9) En déduire la conductance globale U_g de transfert, rapportée au diamètre intérieur.
10) Déterminer dans les conditions d’étude le coefficient de convection de l’eau qu’on notera h_eau.
11) Rappeler l’expression littérale du diamètre hydraulique D_h du tube où circule l’eau et donner son expression littérale simplifiée pour ce cas de figure.
12) A partir du nombre de Nusselt de l’eau (Nu_eau) et en utilisant la bonne corrélation expérimentale, expliciter le diamètre hydraulique de la canalisation où circule l’eau.
13) En déduire le diamètre du système complet (D_systeme).