Une lampe à incandescence produit de la lumière visible à partir d’un filament de tungstène porté à incandescence. Pour éviter une dégradation très rapide du filament, celui-ci est placé dans une ampoule de verre renfermant des gaz à haute pression (voir figure ci-dessous).
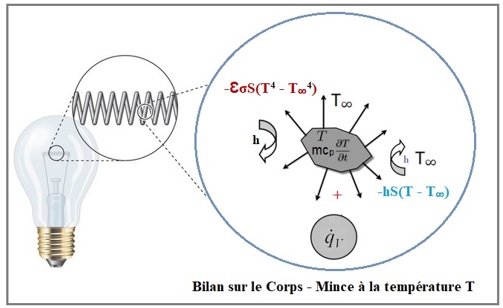
On se propose dans cet énoncé de déterminer le temps de réponse du filament de tungstène dans deux configurations données. Chacune des configurations dépend de la formulation d’une série d’hypothèses. Le filament étudié ici est un fil cylindrique spiralé, assez fin, de diamètre D = 300µm et de longueur L = 1m.
I-) Dans la première configuration, le filament baigne dans un gaz à la température T∞ = 25°C. On note h = 40 W.m-2.K-1, le coefficient d’échange global entre le filament et le gaz. La circulation d’un courant I génère une production de chaleur ohmique : qv = ReI2, avec Re = 4ρeL/πD2, la résistance électrique. Dans cette partie, le rayonnement sera considéré comme négligeable.
On fixe les données suivantes pour le filament de tungstène : ρe = 10-7Ωm ; I = 3A ; ρ = 8000 kg.m-3 ; cp = 500 J.kg-1.K-1 ; λ = 168 W.m-1.K-1 ;
1°) Est-ce que l’approximation de corps mince s’applique pour le filament de tungstène ? Justifier votre réponse
2°) Établir l’équation différentielle régissant l’évolution de la température au sein du filament et exprimer puis calculer la constante de temps τ1 du phénomène.
3°) Partant de l’équation différentielle de la question précédente, donner l’expression du profil de température au sein du filament. On admettra qu’à l’instant initial, T(0) = T∞.
4°) Représenter graphiquement ce profil de température. Faire apparaitre sur ce graphique, la constante de temps τ1 et la température d’équilibre du filament (température atteinte lorsque t tend vers +∞).
II-) Dans la seconde configuration, en plus des hypothèses formulées précédemment, le flux rayonné n’est plus négligé. On posera V le volume du filament et S la surface d’échange avec le gaz. Ɛ = 0,82 est l’émissivité et σ = 5,67.10-8 W.m-2.K-4 la constante de Stefan-Boltzmann.
5°) Quelle est la nouvelle forme de l’équation bilan
On suppose maintenant que l’écart de températures entre le gaz et le filament n’est pas trop grand. Ce qui permet de linéariser la contribution au bilan du rayonnement. Ainsi, si on pose :
T = T∞ + δ, avec δ << 1
6°) Montrer que le flux rayonné peut alors se mettre sous la forme :
ƐσS(T4 – T∞4) = hrS(T – T∞ )
• Exprimer et calculer le coefficient hr. Quel est sa dimension ?
7°) En déduire que l’équation bilan dans la configuration II peut finalement se mettre sous la forme :
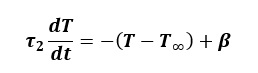
• Exprimer τ2 et β en fonction de h et hr. Faire l’application numérique.
8°) Comparer τ1 et τ2. Conclure
