0212-3ACh6. Modification du coefficient de convection due à l’encrassement dans un tube cylindrique*

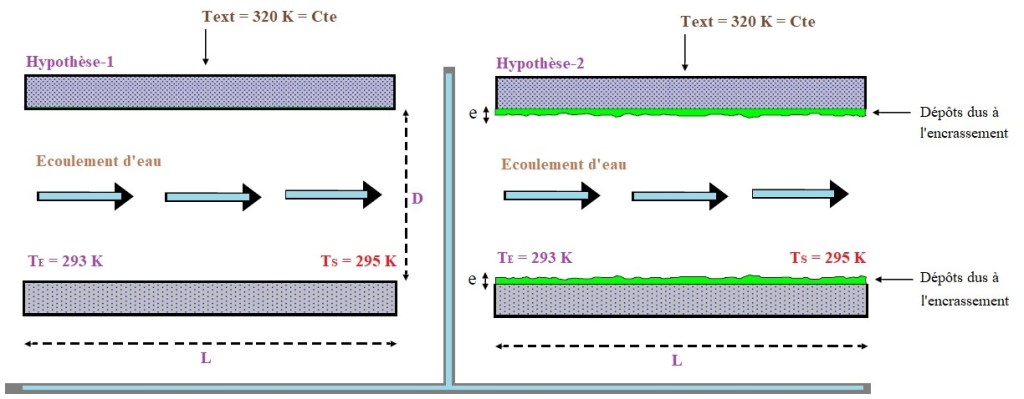
De l’eau s’écoule en régime permanent, à une vitesse moyenne débitante V = 1,5m·s⁻¹ dans une conduite de section droite circulaire, de diamètre intérieur D = 25mm, et de longueur L = 2,5m. L’extérieur du tube est maintenu, sur toute sa longueur, à une température constante de T_ext = 320K. On suppose que la résistance thermique conductive de la paroi métallique du tube peut être négligée. La température de l’eau à l’entrée du tube est de T_E = 293K, tandis que la température mesurée en sortie est de T_S = 295K (voir figure ci-dessous).

On donne :
• La masse volumique de l’eau ρ = 1 000 kg·m⁻³ ;
• La capacité thermique massique de l’eau c_p = 4180 J·kg⁻¹·K⁻¹ ;
• La viscosité cinématique de l’eau ν = 10⁻⁶m²·s⁻¹.

1°) Exprimer, puis calculer, la puissance thermique effectivement transférée à l’eau.
2°) En déduire l’expression du coefficient Conducto-convectif, noté h, de l’échange considéré. Faire l’application numérique.
Compte tenu de la faible température de sortie T_S mesurée, on fait l’hypothèse de l’existence d’un encrassement, déposé sur la paroi interne du tube, créant ainsi une résistance thermique de paroi. On cherche tout d’abord à justifier cette hypothèse en calculant la résistance thermique qu’aurait le tube s’il était propre.
3°) Rappeler les principaux mécanismes physiques associés à la convection et expliquer pourquoi le nombre de Reynolds joue un rôle important. Déterminer le régime d’écoulement de la situation étudiée.

Dans la suite, on suppose que le coefficient Conducto-convectif h_c (W·m⁻²·K⁻¹) peut être calculé pour l’eau, par la relation suivante, prenant en compte les dépendances des propriétés thermophysiques de l’eau avec la température T(K) :

h_c = 1063(1 + 0,00293T)V^0,8D^-0,2 ;

4°) A quelle température doit-on calculer le coefficient h_c ? Justifier votre réponse.
5°) Calculer le coefficient h_c pour cette température. Comparer cette valeur à celle trouvée à la question 2. Conclure.
6°) En déduire la résistance thermique R_d créée par le dépôt interne.
7°) En admettant que ce dépôt est constitué d’un matériau minéral de conductivité thermique : λ = 1.5W·m⁻¹·K⁻¹, calculer l’épaisseur e du dépôt existant sur la paroi interne du tube.