Partie-1 : Étude d’une ailette seule
Soit une ailette en aluminium, de conductivité thermique λ, de profil rectangulaire d’épaisseur e, de longueur L et de largeur l, comme sur la Figure ci-dessous. On note T∞ la température du fluide extérieur balayant l’ailette. Le coefficient de transfert convectif est noté h.
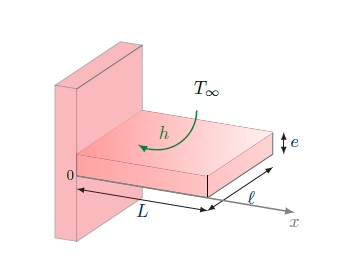
Hypothèses simplificatrices et conditions aux limites :
- Tb est la température à la base de l’ailette (en x = 0).
- En bout d’ailette (ie : x = L), on considère qu’il y a conservation du flux de chaleur (condition de type Newton).
- On se place en régime permanent.
- Il n’y a pas de terme de production de chaleur.
1°) Exprimer le module de l’ailette en fonction des données de l’énoncé uniquement.
2°) En partant de l’équation différentielle de l’ailette, établir l’expression donnant l’évolution de la température au sein d’une ailette. On préconisera ici l’utilisation des fonctions hyperboliques plutôt que des fonctions exponentielles.
3°) Établir l’expression du flux de chaleur dissipé par l’ailette. En déduire l’expression du rendement de l’ailette noté ɳa, en fonction des données de l’énoncé et du module de l’ailette.
Partie-2 : Refroidissement d’une carte de circuit imprimé
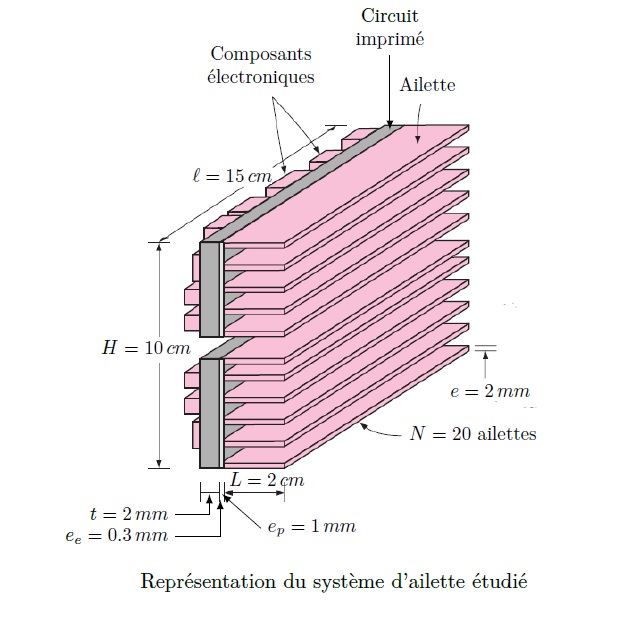
Une carte de circuit imprimé d’épaisseur t = 2mm, de hauteur H = 10cm et de largeur l = 15cm (voir figure ci-dessous), contient des composants électroniques sur une face qui dissipent de manière uniforme, une puissance thermique totale équivalente à Ptot = 15 W. La carte est imprégnée de remplissages métalliques conducteurs et présente une conductivité thermique effective de λc = 12W.m-1.K-1. Toute la chaleur générée par les composants est conduite à travers la carte de circuit imprimé et cette chaleur est dissipée en direction de la face arrière de la carte.
Une plaque en aluminium d’épaisseur ep = 1mm, de hauteur H = 10cm, de largeur l = 15cm, dotée de N = 20 ailettes en aluminium de profil rectangulaire, d’épaisseur e = 2mm, de longueur L = 2cm et de largeur l = 15cm, est fixée sur la face arrière de la carte avec une couche adhésive en époxy, d’épaisseur ee = 0,3mm. La conductivité thermique de l’aluminium est λ = 237W.m-1.K-1, et celle de l’époxy est λe = 1,8W.m-1.K-1.
Le système d’ailettes est balayé par de l’air soufflé à la température T∞ = 37°C avec un coefficient de transfert convectif h = 45W.m-2.K-1. On donne la valeur du rendement d’une ailette ɳa = 0,985; l’expression de ce rendement a été déterminée à la question 3. Comme dans la première partie de cet énoncé, ici aussi le régime est permanent.
4°) Réaliser le schéma électrique équivalent du système complet étudié. Définir les notations introduites pour désigner les différentes résistances thermiques.
5°) Exprimer la résistance équivalente Req en fonction du rendement d’une ailette ɳa et des données de l’énoncé uniquement. Faire l’application numérique.
6°) Exprimer puis calculer la température sur la face avant du circuit imprimé, notée T1.
7°) Exprimer puis calculer la température Tb à la base du système d’ailette, c’est-à-dire à l’interface entre l’ailette et la plaque en aluminium.
8°) Déterminer (expression littérale uniquement) le rendement ɳs et l’efficacité Ɛs du système de N = 20 ailettes étudié.
9°) Sachant que Ɛs = 8,87 ; pensez-vous que l’utilisation d’un tel système d’ailettes soit intéressante ?
