Un procédé de cogénération est un système thermodynamique optimisé afin de produire simultanément de l’électricité et de la chaleur. Ce processus permet d’améliorer l’efficacité énergétique globale en récupérant la chaleur générée dans la production d’électricité et en la réutilisant, par exemple, pour le chauffage ou pour des procédés industriels.
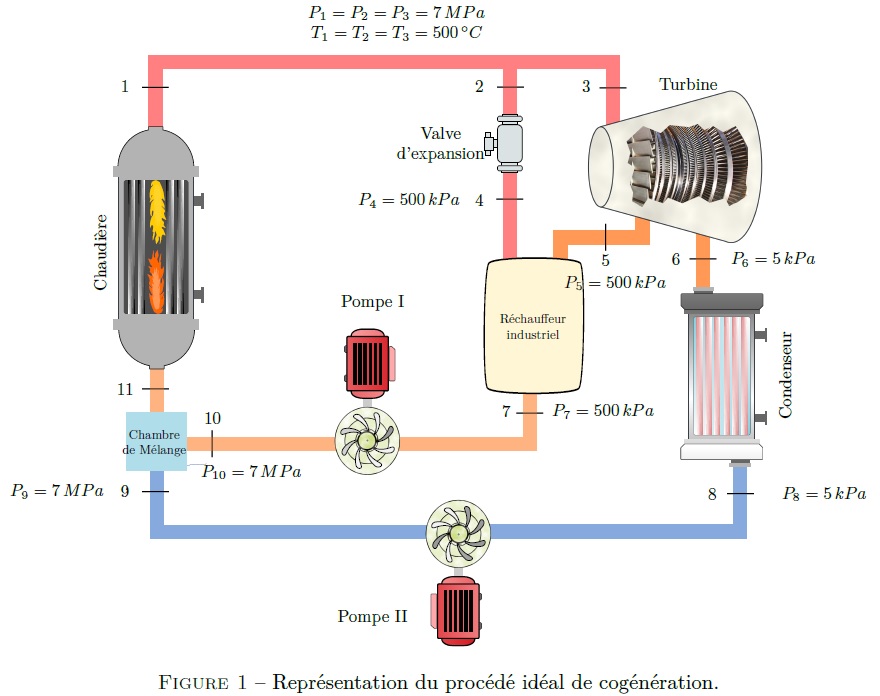
On s’intéresse ici à un procédé idéal de cogénération représenté sur la Figure-1 ci-dessous. Le cycle étudié est également représenté sur la Figure-2. De la vapeur surchauffée entre dans la turbine à la pression P3 = 7MPa et à la température T3 = 500°C. En sortie de turbine, a = 70% du débit massique du mélange liquide vapeur est extrait à la pression P5 = 500kPa (courant 5). Le reste continue à se détendre jusqu’à atteindre la pression P6 = 5kPa. Le mélange liquide vapeur est ensuite condensé à pression constante et pompé, via la pompe II, vers la chambre de mélange à la pression de P9 = 7MPa.
On note D1 = 15kg.s-1 le débit massique traversant la chaudière. Lorsque la demande de chaleur est importante, on injecte b = 10% du débit massique D1 vers la valve d’expansion permettant d’obtenir de la vapeur à une pression de P4 = 500kPa (courant 4). Le fluide provenant des courants 4 et 5 est ensuite injecté vers le réchauffeur industriel. En sortie de ce réchauffeur industriel, le fluide se trouve à l’état de liquide saturé à P7 = 500kPa (courant 7). Il est ensuite pompé via la pompe I à P10 = 7MPa.
Comme hypothèses : on se place en régime permanent; les variations d’énergies cinétique et potentielle sont négligées devant les variations d’enthalpie; on supposera que la transformation 2-4 au travers de la valve d’expansion est isenthalpique et, les transformations subies par le fluide traversant la turbine et les pompes, sont isentropiques (voir également Figure 2).
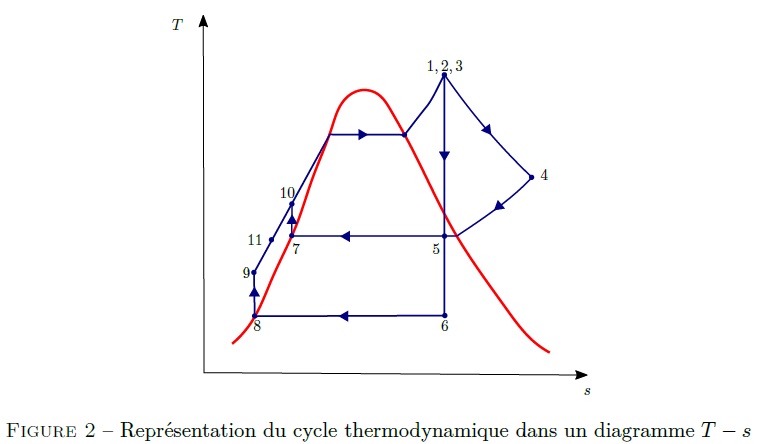
1°) En précisant votre démarche, calculer l’enthalpie h5 en sortie de turbine dans le courant 5. On notera que la transformation 3-5 est isentropique.
2°) A partir d’un bilan de masse à travers toute l’installation, exprimer les différents débits massiques sous la forme : Di = ciD1. Dans cette relation ci, représente un coefficient à déterminer, avec i compris entre 2 et 11. Faire les applications numériques.
3°) Établir l’expression de la puissance produite par la turbine en fonction des enthalpies (h3, h5, h6), du débit massique D1, de a et b. Faire l’application numérique. On donne h6 = 2073 kJ.kg-1.
4°) Exprimer, puis calculer, les travaux massiques (spécifiques) des pompes I et II. Ces expressions devront notamment faire intervenir les variations de pressions.
5°) En déduire le travail net (en Watt) produit par le système étudié.
6°) En appliquant le Premier Principe de la Thermodynamique au niveau de la chambre de mélange, exprimer puis calculer, l’enthalpie h11.
7°) Exprimer la puissance thermique (en Watt) de la chaudière. Faire l’application numérique.
8°) Déterminer ensuite (expression + application numérique), la puissance thermique (en Watt) du réchauffeur de process.
9°) Calculer alors le rendement de cogénération ɳc de l’installation.
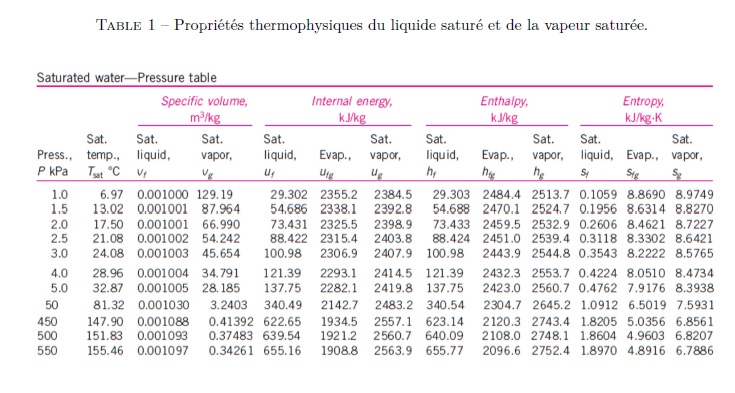
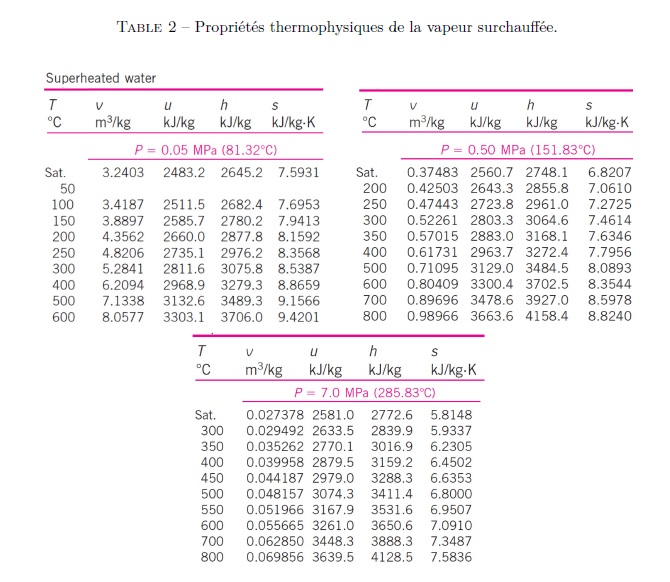
Propriétés thermophysiques des fluides saturés :