L’observation des rayonnements infrarouges provenant de l’espace (des Étoiles jeunes par exemple) peut se faire à l’aide de télescopes. Dans ce domaine de longueurs d’onde, plusieurs difficultés émergent. D’une part, ces rayonnements sont fortement absorbés par l’atmosphère. D’autre part, l’atmosphère et les instruments de mesure émettent également du rayonnement infrarouge. On peut s’affranchir du problème de l’atmosphère en embarquant le télescope sur un satellite et en ce qui concerne le problème de l’émission thermique de l’instrument, on recourt souvent au refroidissant des différents éléments à l’aide de puissants systèmes cryogéniques.
Remarque : L’énoncé est divisé en deux parties indépendantes.
Partie I-Détection de rayonnement infrarouge
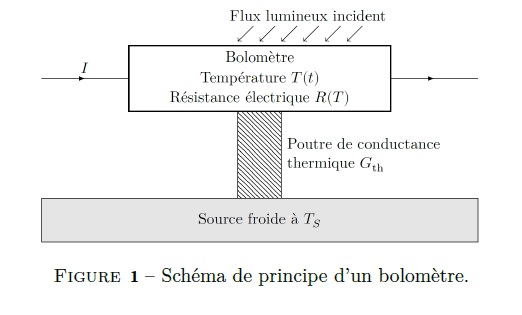
Les rayonnements infrarouges sont détectés par des instruments appelés Bolomètres. Le Principe de la détection repose sur la variation de la résistance d’un matériau lors de son échauffement suite à une absorption de rayonnement électromagnétique. La Figure-1 présente le schéma de principe du Bolomètre étudié. Le Bolomètre, de capacité thermique Cth absorbe le flux radiatif incident Pi supposé constant. Il possède par ailleurs une résistance électrique R(T) fonction de sa température T supposée uniforme et est parcouru par un courant d’intensité I. Ce Bolomètre est relié mécaniquement et thermiquement à une source froide maintenue à la température TS par des poutres de conductance thermique Gth (inverse de la résistance thermique). On mesure les variations de la tension V à ses bornes lorsque la résistance électrique R varie. Cette résistance est reliée à la température en suivant une loi linéaire :
R(T) = R0 + aR0 (T − TS)
Où a < 0 et R0 sont des constantes caractéristiques du matériau.
On rappelle que l’émittance spectrale (ou densité de flux spectrale émis) d’un corps noir à la température T s’écrit :
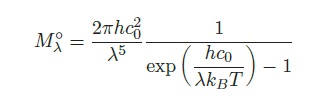
Où h désigne la constante de Planck, kB la constante de Boltzmann, c0 la célérité de la lumière dans le vide et λ la longueur d’onde.
I.1 Généralités sur le rayonnement
1°) Dans quel intervalle de longueur d’onde se situe le rayonnement infrarouge ?
2°) Énoncer la loi du déplacement de Wien relative à l’émission thermique d’un Corps Noir.
3°) Citer deux autres lois utilisées en rayonnement thermique.
4°) Établir l’expression de la Densité de Flux émise M0 ou Émittance d’un corps noir à la température T. On donne :
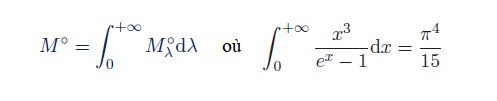
5°) En déduire l’expression de la constante de Stefan-Boltzmann.
6°) Expliquer, en le justifiant avec des valeurs numériques, pourquoi il est nécessaire de refroidir les instruments d’un télescope, qu’il soit sur Terre ou dans l’Espace (température de l’ordre de quelques dizaines de Kelvin).
I.2 Principe du Bolomètre
7°) Montrer que la température T du Bolomètre suit l’équation différentielle :
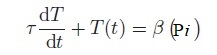
Où l’on exprimera le coefficient τ en fonction des paramètres Gth, a, R0 et I, ainsi que la fonction β(Pi).
8°) Expliquer pourquoi un coefficient a négatif garantit la stabilité du fonctionnement du dispositif.
9°) Déterminer, en fonction des données de l’énoncé, la température Tp(Pi) du Bolomètre qui reçoit un flux Pi en régime permanent.
I.3 Temps de réponse du bolomètre
On s’intéresse, ici, au temps de réponse du Bolomètre. Pour cela, le système étant en équilibre thermique sous le flux radiatif incident Pi, on supprime brutalement ce flux radiatif incident à l’instant t = 0.
10°) Déterminer l’expression de T(t) en fonction des données de l’énoncé et tracer l’allure de l’évolution T(t). On précisera sur le graphe la signification de la constante τ.
11°) Expliquer qualitativement l’influence de la capacité thermique Cth et de la conductance thermique Gth sur le temps de réponse du bolomètre.
Partie II-Refroidissement cryogénique du télescope Herschel
Le refroidissement cryogénique est une technique utilisée afin d’atteindre des températures très basses. Ce principe de refroidissement est mis à profit dans les Cryo-réfrigérateurs à adsorption. Ces dispositifs de refroidissement ne contiennent aucune partie mobile, ce qui les rend parfaitement adapté aux contraintes spatiales.
Schématiquement, le Cryo-réfrigérateur se présente sous la forme de deux sphères en titane reliées par un tube. Dans l’une des sphères appelée ‘Pompe‘, se trouve du charbon actif. Ces charbons possèdent un pouvoir d’adsorption du gaz qui augmente lorsque la température diminue. La Pompe peut être reliée à un thermostat de température Ti = 2K par un interrupteur thermique ou chauffé à la température Tc = 45K par une chaufferette électrique. L’autre sphère est appelée évaporateur. Elle contient une mousse qui permet de retenir le liquide par capillarité en l’absence de pesanteur.
Le dispositif fonctionne à l’aide d’interrupteurs thermiques permettant de connecter ou déconnecter certaines parties afin de laisser passer ou non la chaleur. L’interrupteur thermique à gaz tire partie de la conduction des gaz pour assurer sa position fermée. Il est composé (voir Figure-2) de deux pièces conductrices cylindriques concentriques en cuivre de rayons R1 et R2 > R1. L’espace entre les deux cylindres peut être vide ou rempli d’hélium gazeux. On négligera les forces de pression et les transferts thermiques par rayonnement et convection et les effets de bord.
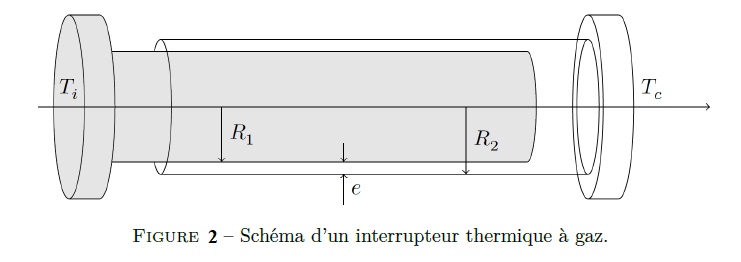
12°) Établir l’équation de diffusion de la chaleur en l’absence de terme source.
13°) Établir, pour la situation étudiée, l’expression de la température T(r) en régime permanent.
14°) En partant de la définition du flux thermique, déterminer, en régime permanent, l’expression de la puissance thermique Pi à travers un cylindre de rayon r et de hauteur H. Que peut-on en conclure ?
15°) Exprimer la conductance thermique G de l’interrupteur fermé en fonction des données du problème.
16°) Expliquer qualitativement comment ce dispositif peut jouer le rôle d’interrupteur thermique.
