Le Harfang des neiges (voir Figure-01), appelé aussi Chouette Harfang, est un oiseau qui vit principalement dans la toundra arctique. L’objectif de ce problème est d’étudier la capacité des harfangs à résister au froid rigoureux et aux vents parfois violents qui règnent dans la toundra en hiver.

Partie I-Conduction thermique
Pour établir des bilans énergétiques sur la chouette harfang, il est nécessaire d’étudier une géométrie définissant un volume corporel fini. Un modèle très simplifié, mais fournissant malgré tous des résultats qualitativement significatifs, est constitué par une géométrie sphérique. On suppose que le corps de l’oiseau est une sphère homogène de centre O, de rayon R et de masse volumique ρ, maintenue à la température corporelle Ti. Il est enveloppé par une couche isolante d’épaisseur e représentant le plumage. La distance au centre O est repérée par la coordonnée radiale r. On étudie la conduction thermique dans le plumage, de conductivité thermique λ, avec comme conditions aux limites : T(r = R) = Ti et T(r = R + e) = Te. La température Te < Ti est la température extérieure (ambiante). Il n’y a pas de source volumique dans le plumage.
1°) Justifier que la température ne dépend que de r et en déduire l’expression du vecteur densité de flux thermique dans le plumage. Préciser la direction et le sens de ce vecteur, ainsi que la dimension de sa norme.
2°) Établir l’expression de la température dans le plumage.
3°) Établir l’expression du flux thermique à travers une sphère de centre O et de rayon r compris entre R et R + e. Qu’en déduisez-vous ?
4°) Exprimer la conductance thermique Gth du plumage. On rappelle que la conductance thermique est l’inverse de la résistance thermique.
Partie II-Taille de l’oiseau et résistance au froid
5°) En notant m la masse corporelle (sans le plumage) de l’oiseau, on définit la conductance thermique rapportée à l’unité de masse corporelle par : Gm = Gth/m. Expliquer pourquoi Gm est une grandeur pertinente pour estimer les capacités de résistance au froid d’un animal.
6°) Établir l’expression de Gm pour le plumage en géométrie sphérique en fonction de λ, R, e et ρ.
On compare deux oiseaux de masses corporelles respectives m1 et m2. On suppose que les corps de ces oiseaux sont sphériques, de même masse volumique ρ et qu’ils ont la même épaisseur de plumage e, les conductivités thermiques étant aussi les mêmes.
Données : e = 1 cm, m1 = 2 kg, m2 = 10 g, ρ = 1000 kg·m-3
7°) Exprimer puis calculer numériquement le rapport x = Gm1/Gm2 des conductances thermiques par unité de masse corporelle des deux oiseaux, notées respectivement Gm1 et Gm2.
8°) En analysant les résultats obtenues et fournies par l’énoncé, discuter l’effet de la taille sur la capacité des oiseaux à vivre dans des climats très froids en considérant une épaisseur de plumage constante.
Partie III- Influence du vent
Lors d’une étude expérimentale, des harfangs des neiges ont été placés dans des cages et soumis à différentes températures ambiantes Ta ainsi qu’à un vent de vitesse V. La consommation de dioxygène par ces oiseaux a été mesurée sur une durée de 2 à 4 heures après que la température ambiante se soit stabilisée. On note CV la consommation de dioxygène par unité de masse corporelle lorsque la vitesse du vent est V et C0 celle en l’absence de vent (V = 0). À une température ambiante donnée, une série d’expériences a permis de postuler la loi suivante :
CV – C0 = AVβ eq-01
Avec A et β deux paramètres pouvant dépendre de la température ambiante. Une série de mesures a été réalisée avec une vitesse de vent V1 = 4,47 m/s et une autre avec une vitesse de vent V2 = 7,47 m/s.
Pour la vitesse V1, une régression linéaire pour les mesures de consommation de dioxygène (en cm3/g/h) en fonction de la température ambiante Ta (en °C) a donné la loi suivante :
C1 = C0 + 0,260 – 0,0193Ta eq-02
Pour la vitesse V2, la loi obtenue est :
C2 = C0 + 0,337 – 0,0251Ta eq-03
9°) Déterminer la valeur de l’exposant β de l’eq-1 pour Ta = 0°C et Ta = −40°C. Conclure.
La consommation d’énergie d’un harfang peut être déterminée à partir des mesures de volumes de dioxygène consommé (notamment via eq-1). On souhaite maintenant vérifier la dépendance de la consommation d’énergie avec la vitesse du vent (dépendance en Vβ d’après eq-1) en passant par le calcul du flux thermique dissipé par l’oiseau. Pour cela, on étudie une plaque plane en contact sur un de ses côtés avec de l’air animé d’une vitesse V. La température de surface de la plaque est TS. La température de l’air est égale à Ta < TS, sauf dans une fine couche, appelée couche limite thermique, au voisinage de la plaque où la température varie rapidement de TS à Ta.
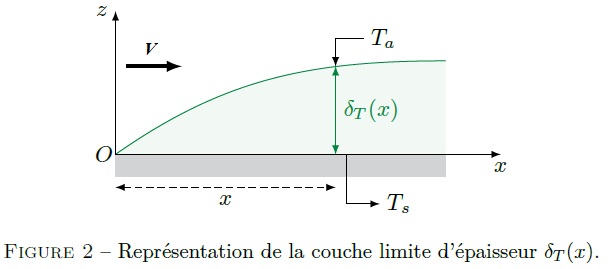
On suppose que la variation de température dans la couche limite thermique est due au phénomène de conduction thermique. De plus, on suppose que la couche limite est suffisamment fine pour pouvoir considérer que la diffusion thermique n’a lieu que dans la direction Oz orthogonale à la plaque. Enfin, on admet que l’épaisseur de la couche limite thermique se met sous la forme :
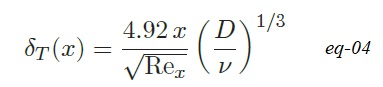
Où Rex est le nombre de Reynolds local de l’écoulement à l’abscisse x, défini avec la vitesse caractéristique V, la longueur caractéristique x, D la diffusivité thermique de l’air et ν la viscosité cinématique de l’air.
10°) Considérons un élément de surface dS de largeur dx selon Ox et de longueur a dans la direction orthogonale au plan de la Figure 2 : dS = adx. Exprimer le flux thermique dΦ à travers la couche limite thermique à l’abscisse x en fonction de dS, V, D, ν, x, TS, Ta et de la conductivité thermique de l’air λa.
11°) Montrer que le flux thermique total sortant de la plaque entre x = 0 et x = L peut s’écrire :
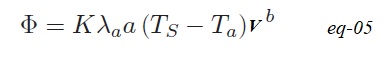
Où K et b sont deux constantes à exprimer.
12°) Comparer la valeur de l’exposant b à celle de β, déterminée à la question 9.
