0223-4ACh3. Étude d’un procédé de récupération de chaleur des eaux usées*

On s’intéresse ici à un procédé de récupération de chaleur provenant des eaux usées dont la température est de l’ordre de 16°C. Un échangeur thermique est directement placé dans les collecteurs.

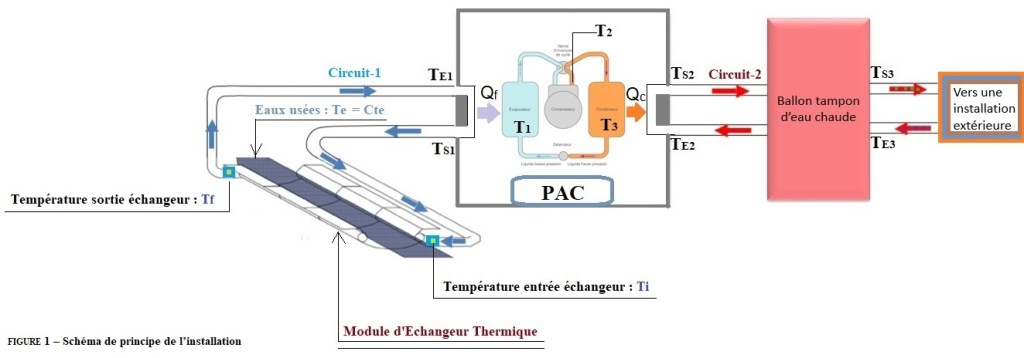
Le schéma de principe de l’installation est représenté Fig-1. Il est composé de :

• De modules thermiques représentant un échangeur placé dans les collecteurs d’eaux usées
• Une Pompe à Chaleur (PAC)
• Un ballon tampon d’eau chaude

Partie I – Étude de la pompe à chaleur ou PAC

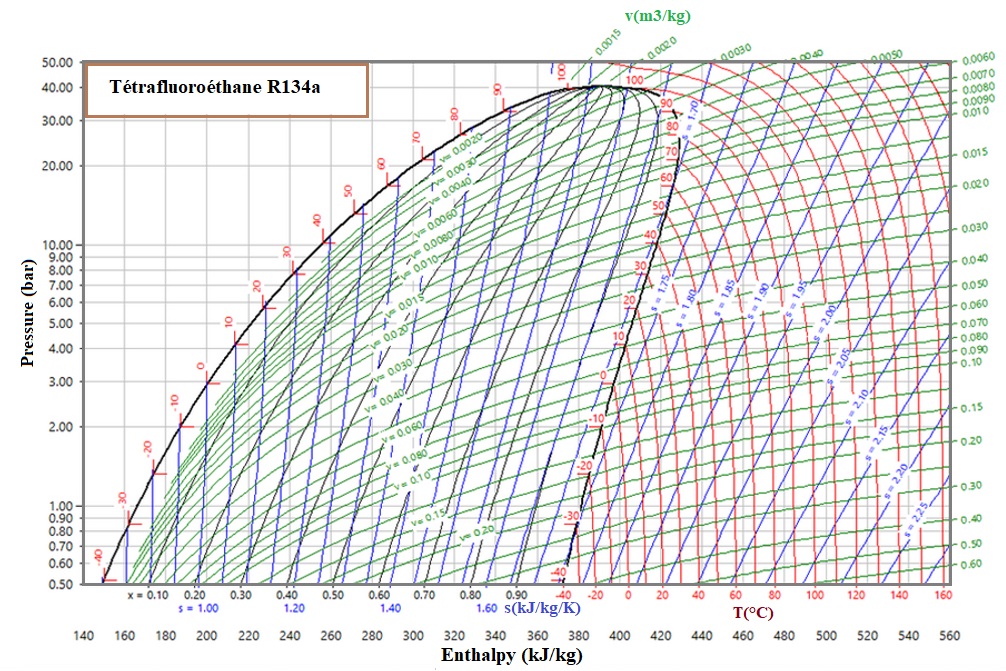
Le principe de fonctionnement de la PAC est représenté Fig-2. Le fluide caloporteur utilisé est du Tétrafluoroéthane-R134a. Ce fluide entre dans le compresseur à la température T₁ = 10°C   et à la pression P₁ = 3,5 bars. En sortie du compresseur, la pression est P₂ = 14 bars. La température en sortie du condenseur est T₃ = 50°C. La puissance prélevée à la source froide est ϕ_froid = 60 kW. La puissance fournie au compresseur est ϕ_comp = 19 kW.

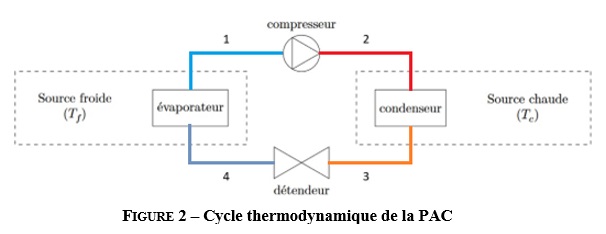
Les transformations suivies par le fluide caloporteur dans la PAC sont les suivantes :

• Transformation 1 à 2  : compression isentropique ;
• Transformation 2 à 3  : 1^er refroidissement, puis changement d’état complet suivi d’un 2^e refroidissement isobare pour atteindre la température T₃;
• Transformation 3 à 4  : détente isenthalpique ;
• Transformation 4 à 1 : vaporisation complète suivi d’un échauffement isobare pour atteindre la pression P₁.

1°) Tracer le cycle Thermodynamique de la PAC dans le Diagramme Enthalpique fourni en fin d’énoncé.

2°) Indiquer les états du fluide dans les courants 1, 2, 3 et 4. Quel est l’intérêt d’utiliser le fluide dans l’état où il apparaît dans le courant 1.

3°) Appliquer le Premier Principe au niveau de l’évaporateur et justifier toutes les simplifications introduites. En déduire l’expression du débit massique du fluide caloporteur circulant dans la PAC. Faire l’application numérique.

4°) Déterminer le Titre massique en vapeur au point 4.

5°) Exprimer l’Efficacité de condensation ou COP_cond de la PAC. Faire l’application numérique.

Partie II – Dimensionnement simplifié de l’échangeur du collecteur

L’échangeur repose sur le fond de la conduite cylindrique d’eaux usées, comme indiqué sur la Figure-3. La Fig-3.a présente un tronçon d’échangeur de 1m de long. On réalise ainsi un module d’échangeur de longueur L₀ par mise en série de tronçons de 1m.

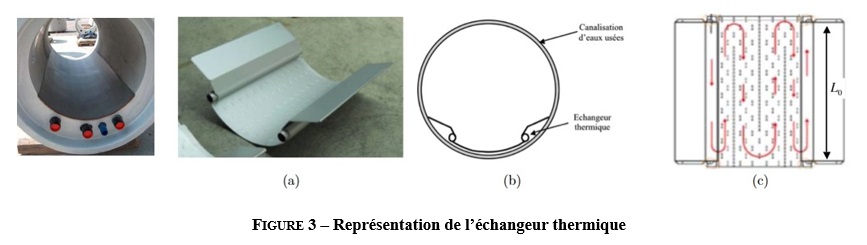
Après mise en série des tronçons, le fluide circule dans le module selon le schéma représenté Fig-3.c (vue de dessus du module). Il se réchauffe progressivement au contact des eaux-usées, de température T_e supposée uniforme et constante. On supposera pour simplifier que l’échange thermique se fait uniquement sur la partie métallique incurvée (voir Fig-3.a), ce qui correspond à deux aller-retours, soit N = 4 passages du fluide sur la longueur du tronçon considéré. Le module est donc équivalent au schéma représenté à la Fig-4.

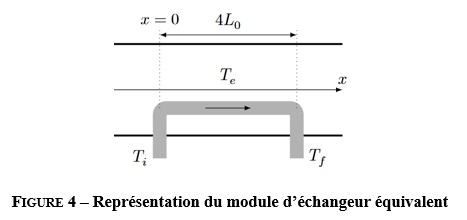
Hypothèse de l’étude :

• L’écoulement est supposé parfait, permanent, unidimensionnel, de variations d’énergies cinétique et potentielle négligeables ;
• Le fluide entre dans l’échangeur à la température T_i = 12,5 °C et en ressort à la température T_f  = 15,5 °C ;
• On note   q_m0, le débit massique dans un module  d’échangeur,   c_e = 4180 Jkg^-1K^-1 la capacité thermique massique de l’eau.
• On impose la température des eaux usées à T_e = 16°C, constante.
• On supposera que la PAC est parfaitement calorifugée.

Ces hypothèses correspondent au fonctionnement hivernal. On notera de plus U = 914 Wm^-2K^-1, le coefficient d’échange thermique global au sein de l’échangeur. D = 5cm est le diamètre de la conduite dans un module d’échangeur au sein duquel, la surface d’échange sera assimilée à l’enveloppe d’un cylindre de diamètre D  et de longueur 4L₀. En tenant compte des pertes thermiques et mécaniques (pertes de charge) dans les canalisations du circuit 1 (voir Fig-1), les températures en entrée et en sortie de l’évaporateur sont données par :  T_E1 = 15°C et T_S1 = 13°C.

6°) En justifiant vos simplifications, appliquer le Premier Principe à l’eau circulant dans le circuit 1 et déterminer son débit massique q_m1 en fonction notamment des températures T_E1 et T_S1, ainsi que du flux ϕ_froid. Faire l’application numérique.

7°) L’installation est constituée de N_m = 45 modules d’échangeurs indépendants (i.e. correspondant à une association parallèle), posés les uns à la suite des autres sur une longueur totale L. On rappelle que chaque module d’échangeur correspond à une longueur L₀. Ainsi, L = N_mL₀. Déterminer l’expression du débit massique q_m0 en fonction de  q_m1 et N_m.

8°) Exprimer la puissance reçue par l’eau circulant dans un module d’échangeur en fonction de q_m0, c_e, T_i  et T_f.

9°) Déterminer l’expression de la longueur L₀ d’un module d’échangeur en fonction notamment de U, q_m0  et des températures.

10°) Calculer la longueur totale L de l’échangeur. Commenter le résultat obtenu.