Partie I : Généralités sur la conduction thermique
Considérons un milieu métallique continu, isotrope, homogène constitué de cuivre. On note ρ la masse volumique du cuivre, c sa capacité thermique massique, λ sa conductivité thermique et Dth sa diffusivité thermique. Toutes ces grandeurs sont uniformes et constantes au cours du temps. Les échanges thermiques au sein du milieu s’effectuent exclusivement par conduction. En outre, on supposera que le problème de conduction est unidimensionnel selon la direction x, toute grandeur dans le milieu métallique ne dépendra spatialement que de x.
1-) A partir d’un bilan énergétique, montrer que le profil de température T = T(x, t) dans le milieu considéré est donnée par l’équation différentielle :
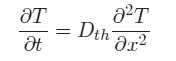
Où, Dth est à exprimer en fonction de ρ, c et λ. Préciser l’unité de Dth.
2-) Déterminer, en le justifiant, l’ordre de grandeur de la durée d’établissement ζcd du régime permanent d’un phénomène diffusif dans un milieu de diffusivité thermique Dth et pour une extension spatiale l. Calculer ζcd pour Dth ≈ 10-4 USI et l ≈ 1m. Commenter le résultat.
Partie II : Détermination expérimentale de la conductivité thermique et de la diffusivité thermique du cuivre
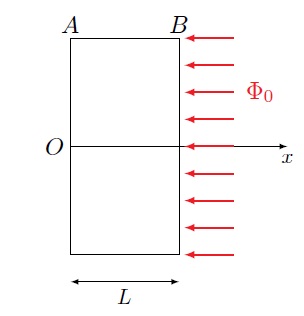
La détermination expérimentale de l’une des grandeurs λ ou Dth nécessite d’appliquer des échelons de température ou de flux thermique sur l’une ou les deux faces d’un échantillon massif, qu’il soit de dimension semi-in finie ou finie, et d’étudier l’évolution de la température en régime instationnaire. Considérons une lame parallélépipédique de cuivre de section carrée d’aire S et d’épaisseur L, orientée perpendiculairement à la direction Ox, comme le montre Figure ci-dessous et initialement à la température uniforme T0 = 20°C. La face arrière B(x = L) est soumise, à l’instant t = 0, à une densité de flux de chaleur constante φ0 uniformément répartie, tandis que la face avant A(x = 0) est supposée parfaitement isolée (de même que les faces latérales de la lame).
Deux thermocouples enregistrent les variations au cours du temps des températures TA(0, t) et TB(L, t) des faces respectives A et B. Le dispositif est placé dans une enceinte afin d’éviter tout échange thermique de type convectif avec l’air environnant. La répartition de température T(x,t) est une solution de l’équation de la chaleur. Pour une lame de faible épaisseur L et tant que le temps de mesure demeure inférieur à L2/(2Dth), cette répartition s’écrit sous la forme d’une série infinie :
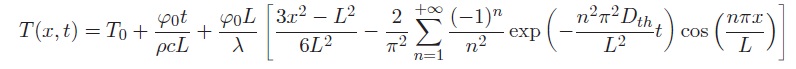
3-) Vérifier que l’expression de T(x, t) est bien solution de l’équation de diffusion de la chaleur.
Expérimentalement, au bout d’un temps t1 = 20 s, on constate que les accroissements de température TA(0, t) – T0 et TB(L, t) – T0 enregistrés évoluent quasi linéairement avec le temps. De plus, au bout d’un temps t2 = 45 s, les relevés de températures fournissent respectivement TA(0, t2) = 270,0°C et TB(L, t2) = 292,7°C. Au-delà du temps t3 = 60 s, un obturateur vient occulter le flux thermique sur la face B. Dans la suite, l’intervalle de temps considéré est t2 = [t1, t3].
4-) Un calcul numérique des premiers termes de la série montre que les termes de la série en exponentiel et cosinus sont négligeables devant les autres :
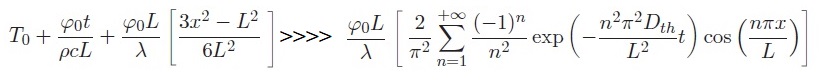
Sous ces hypothèses, écrire les quantités TA(0, t) − T0 et TB(L, t) − T0 en fonction de φ0, L, ρ, c, λ et t.
5-) Représenter TA(0, t) − T0 et TB(L, t) − T0 en fonction du temps t. Commenter.
6-) À partir des équations obtenues à la question 4, déterminer une expression de la conductivité thermique λ qui ne fait pas intervenir la capacité thermique massique c inconnue.
7-) Exprimer la quantité [TB(L, t) − T0] + 2[TA(0, t) − T0] et en déduire l’expression de la capacité thermique massique c du cuivre.
8.-) Calculer λ, puis c, puis la diffusivité thermique Dth. On donne φ0 = 60W·cm−2, L = 3 cm et ρ = 8 960 kg·m−3.
9-) La densité de flux thermique est connue à 1% près alors que les températures sont mesurées à 0,1°C près, et l’épaisseur L à 0,1mm près. Déterminer la précision obtenue sur la détermination de λ.
