0204-2ACh2. Déséquilibre mécanique et thermique d’un gaz parfait*

Principe de Carnot : Toute évolution spontanée génère une création d’entropie

I. Déséquilibre mécanique d’un gaz parfait

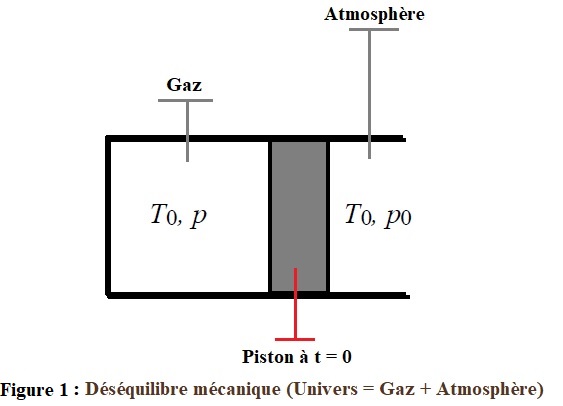
Un corps de pompe horizontal contient une mole de gaz parfait dans les conditions de température et de pression T₀ et p. La capacité thermique molaire C_pm du gaz à pression constante ne varie pas. Le piston et le corps de pompe sont de bons conducteurs thermiques (parois diathermanes). Ainsi :

• A l’état initial, le gaz sous pression p, à la température T₀, occupe un volume V₀
• A l’état final, le gaz sous pression p₀, à la température T₀, occupe un volume V

L’atmosphère est une source d’énergie thermique et de travail. Sa température est notée T₀ et sa pression p₀. Elle peut ainsi, d’une part échanger une quantité finie d’énergie thermique sans voir varier sa température, d’autre part changer de volume sans que sa pression ne varie (la pression et la température au sein de l’atmosphère sont donc toujours constantes). Le piston (Figure 1) est débloqué à l’instant t = 0, à partir de cet instant, il est libre de se déplacer sans frottement jusqu’à l’équilibre thermodynamique. 

On fait l’hypothèse dans tout cet exercice, que l’Univers (Gaz + Atmosphère) est un système isolé.

1-) Établir que d’une manière générale, l’expression de la variation d’entropie d’une mole de gaz parfait en variable (T,p), subissant une transformation réversible entre deux états 1 et 2 ( R étant  la constante des gaz parfaits ou constante molaire),  peut se mettre sous la forme :

∆S = S₂ – S₁ = C_pmln(T₂/T₁) – Rln(P₂/P₁)

2-) Quelle est la variation d’entropie du gaz (∆S_gaz-1) à l’intérieur du corps de pompe ? Précisez son signe selon que p > p₀ ou p < p₀ ? L’évolution du gaz n’est-elle pas irréversible dans les deux cas ?

3-) Calculer la variation d’entropie de l’Univers (∆S_univers-1) et exprimer cette dernière en fonction de x = p₀/p  

4-) À l’aide d’une étude graphique où vous représenterez les fonctions :

f₁(x) = x – 1   et    f₂(x) = ln(x)

• Déterminer le signe de (∆S_univers-1) dans les deux cas (p > p₀ et p < p₀)

II. Déséquilibre thermique du gaz parfait

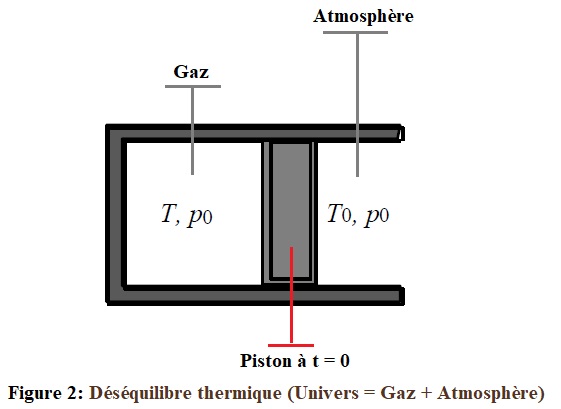
La géométrie du système est la même que la précédente, mais le piston et le corps de pompe sont maintenant recouverts d’un isolant thermique. Le gaz est dans les conditions de température T et de pression p₀. Le piston est libéré à l’instant t = 0 et l’isolant est supprimé (Figure 2). Ici le piston reste fixe, une fois l’isolant supprimé, la chaleur est transférée entre l’atmosphère et le gaz au travers des parois diathermanes.

5-) Exprimer la variation (∆S_gaz-2) de l’entropie du gaz en fonction de T et de T₀.

6-) Exprimer la variation d’entropie de l’Univers (∆S_univers-2). Toujours en procédant graphiquement (en posant cette fois x = T/T₀), déterminer le signe de (∆S_univers-2) dans les deux cas T > T₀ et T < T₀.