I-Première Partie : Questions de Cours
1°) Donner un énoncé du 2nd Principe de la Thermodynamique. Qu’apporte-t-il de plus que le 1er Principe ?
2°) Rappeler les expressions des deux identités Thermodynamiques (ou équations de Gibbs) et préciser leur domaine de validité
3°) A partir d’une des deux identités Thermodynamiques, exprimer la variation d’entropie d’une phase condensée (solide ou liquide).
4°) On considère un système constitué de n moles d’un gaz réel, dont l’équation d’état est définie par le modèle de Clausius suivant :
P(V – nb) = nRT
Avec b, une constante et R la constante des gaz parfaits. On admettra que pour ce système, la fonction Enthalpie obéit à la loi :
H = 5/2 nRT + nbP + H0
Où, P représente la pression du gaz et H0 une constante.
Exprimez la variation d’entropie de ce gaz réel ΔS, entre les états initial et final, en variables (T, P). Il pourrait être nécessaire d’introduire la deuxième identité Thermodynamique ou deuxième équation de Gibbs.
II-Deuxième Partie : Influence de la Précision des Calculs sur la Variation d’entropie d’un système
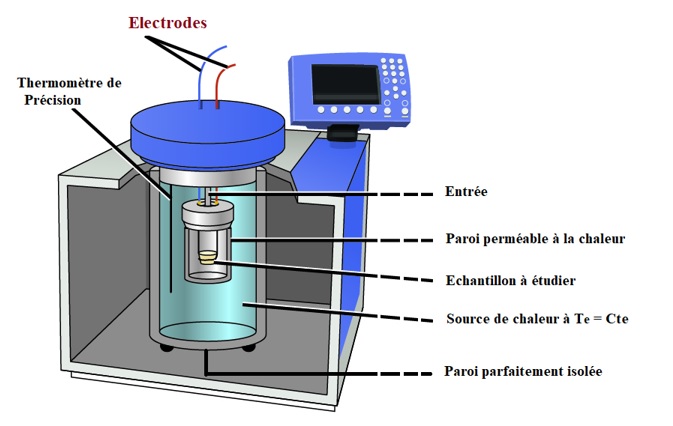
Un solide de masse m et de capacité thermique massique c initialement à T0, est mis en contact thermique avec une source de chaleur de température Te invariable (voir figure ci-dessous). On considère que le système global « source + solide » est parfaitement isolé.
Exprimer entre l’état initial et l’état final :
5°) La variation d’entropie du solide ΔSsolide (expression qui pourrait être simplement et aisément déduite de la question 3).
6°) La variation d’entropie de la source ΔSsource.
7°) La variation d’entropie de l’univers ou entropie créée ΔScréée.

8°) Dans le cas où Te = T0(1 + Ɛ), avec Ɛ << 1, calculer ΔScréée à l’aide de développements limités d’ordre 1 et interpréter le résultat.
9°) En reprenant le cadre de la question précédente et à l’aide de développements limités à l’ordre 2 cette fois, calculer et discuter du signe de ΔScréée.
