Pour refroidir un débit de 9,4 kg/h d’air de 576 °C à 178 °C, on le fait passer dans le tube central d’un échangeur bitube à contre-courant en cuivre de longueur L, de diamètre Di = 2 cm, d’épaisseur e = 1 mm (voir figure ci-dessous) et on prendra la conductivité du cuivre égale à λCu = 401 W.m-1.K-1 et heau = 500 W.m-2.K-1, le coefficient d’échange convectif côté eau.
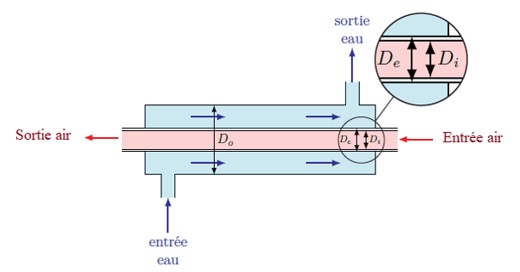
Les propriétés Thermo-physiques de l’air seront prises à une température moyenne, entre les températures d’entrée et de sortie. Un formulaire donnant les corrélations empiriques de Nusselt et une table des propriétés Thermo-physiques sont fournis en fin d’énoncé.
1°) Déterminer (expression et application numérique), la puissance calorifique évacuée par le fluide chaud.
2°) Le fluide de refroidissement est de l’eau, qui pénètre dans la section annulaire à la température de 16°C, avec un débit volumique de 0,6 l/min. Calculer la température de cette eau en sortie d’échangeur. On prendra pour l’eau : CP = 4180 J/kg°C.
3°) Exprimer, puis calculer, le coefficient de transfert convectif hair de l’air. Une attention particulière sera accordée à tous les développements conduisant au résultat.
4°) Exprimer le coefficient d’échange globale Ug rapporté au diamètre extérieur du tube intérieur (De). Faire l’application numérique.
5°) Faisant appel à la différence logarithmique de température, en déduire la longueur du dispositif.
6°) Déterminer (expression et application numérique) l’efficacité Ɛ1 de l’échangeur. S’agit-il d’une efficacité de refroidissement ou de chauffage ? justifier votre réponse.
7°) Après un an de fonctionnement, une résistance d’encrassement Rth = 4.10-4 W-1.m2.K s’intercale entre la face extérieure du cylindre intérieur et l’eau. On supposera inchangé la surface d’échange (toujours rapportée à De). Déterminer (expression et application numérique), le nouveau coefficient d’échange global.
On cherche maintenant à estimer la nouvelle efficacité de l’échangeur notée Ɛ2, après un an d’utilisation et en présence d’encrassement. Pour cela, on utilisera la méthode de NUT (Nombre d’Unité de Transfert) rappelée ci-dessous :

8°) Déduire de ce qui précède, la nouvelle efficacité Ɛ2. Faire la comparaison avec Ɛ1 et conclure.


Bonjour, je suis un étudiant algérien. Je cherche une personne qui pourrait me donner quelques livres en français qui traitent de ce chapitre/module. Merci!
J’aimeJ’aime