Un transistor a la forme d’un disque de rayon R = r + e = 8 mm. Il est monté à la surface d’un milieu isolant et dissipe une puissance thermique de 0,25 W. Pour réduire la température, on lui attache un tube cylindrique creux en cuivre de hauteur L = 15 mm, d’épaisseur e = 0,25 mm de rayon intérieur r = 7,75 mm et de conductivité thermique k = 400 Wm-1K-1 (voir Figure ci-dessous). L’air ambiant est à température Tair = 25°C, le coefficient d’échange convectif est h = 50 Wm-2K-1. On néglige tous les échanges de chaleur à l’intérieur du tube (la dissipation ne se ferait donc que sur la partie externe de l’ailette). De plus, en bout d’ailette (z = L) on supposera une condition de type Newton.
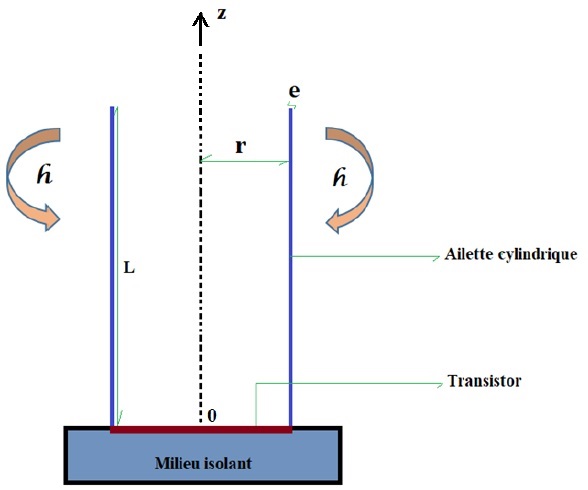
1°) Déterminer la loi d’évolution de la température le long de l’ailette, on supposera qu’au sein de cette ailette le transfert de chaleur par conduction se fait majoritairement dans la direction (oz). Quelle est la température du Transistor (température à la base de l’ailette) ? Quelle serait cette température s’il n’y avait pas eu d’ailette ?
2°) Quel est le flux dissipé par l’ailette cylindrique creuse
3°) Déterminer l’efficacité ou performance de cette ailette, peut-on dire que cette dernière est performante ?
4°) Définir et calculer le rendement de cette ailette
On suppose maintenant qu’on a affaire à une ailette infinie (rapport e/L, très faible). La condition de Newton en bout d’ailette n’est plus alors appliquée. Cependant on maintient ici la condition de Neumann en z = 0 (condition de flux constant, 0,25 W).
5°) A partir des modèles de la littérature, exprimer le flux dissipé par une ailette infinie (aucun calcul n’est nécessaire). En déduire alors l’expression du rendement de cette ailette, si elle avait été infinie.
6°) Y a t-il un intérêt à rallonger indéfiniment la longueur L de l’ailette ? Justifier votre réponse.

joli vos dessins, on voit que vous y consacrez du temps!
J’aimeJ’aime
Très bel exemple merciii!
J’aimeJ’aime
Bel exemple
J’aimeJ’aime