On désigne par P, la pression du système liquide-vapeur et par v, son volume massique.
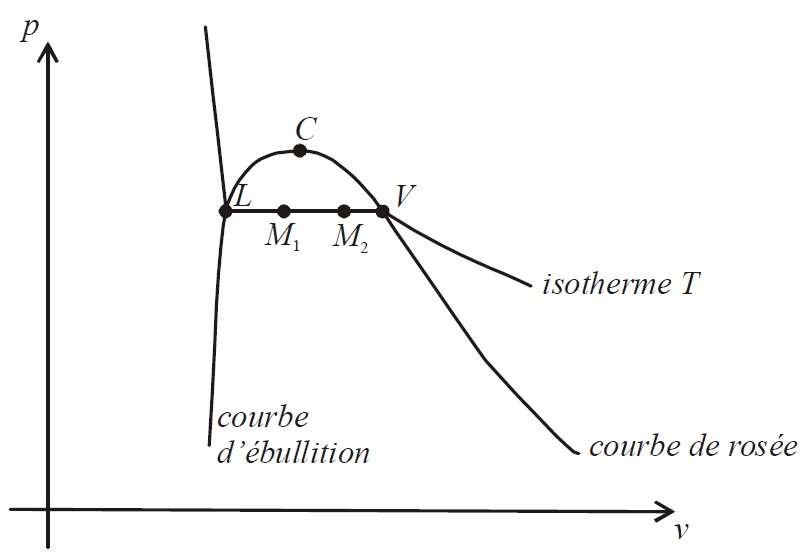
1-) Représenter l’allure du diagramme de Clapeyron (P,v) de l’eau. Représenter sur ce même diagramme l’allure de l’isotherme critique Tcri et l’allure d’une isotherme quelconque T < Tcri.
2-) Indiquer sur le diagramme, les domaines liquide (L), liquide-vapeur (L+V) et vapeur (V).
3-) Justifier et commenter la présence d’un palier sur l’isotherme T < Tcri.
On rappelle que le titre massique en vapeur x d’un système liquide-vapeur est égal au rapport entre la masse mV de vapeur saturante et la masse totale m = mV + mL du système. On désigne respectivement par :
- vL = volume massique du liquide saturant
- hL = enthalpie massique du liquide saturant
- SL= entropie massique du liquide saturant
- vV = volume massique de la vapeur saturante
- hV = enthalpie massique de la vapeur saturante
- SV = entropie massique de la vapeur saturante
- v = volume massique du système liquide-vapeur
- h = enthalpie massique du système liquide-vapeur
- S = entropie massique du système liquide-vapeur
4-) Démontrer le Théorème des moments suivant :
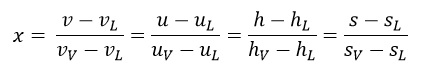
5-) Déterminer les variations d’enthalpie et d’entropie massiques pour un liquide incompressible (point situé sur la courbe d’ébullition).
6-) Déterminer les variations d’enthalpie et d’entropie massiques entre deux points M1 et M2 (voir figure ci-dessous), du palier d’équilibre liquide-vapeur. On posera la chaleur latente massique de vaporisation : lv(T) =hV – hL
7-) Représenter l’allure du diagramme Entropique (T,S) de l’eau. Représenter sur ce même diagramme l’allure de l’isobare critique Pcri et l’allure d’une isobare quelconque P < Pcri.

Very important exercise to become familiar with multiphase flow modelling
J’aimeJ’aime
très bel exemple et surtout problème bien posé
J’aimeJ’aime
Didactique votre approche, merci
J’aimeJ’aime
bien posé!!
J’aimeJ’aime
belle approche didactique
J’aimeJ’aime
Excellent ce petit rappel de cours, pas toujours la modélisation des écoulements multiphasiques
J’aimeJ’aime